给你 k 枚相同的鸡蛋,并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。
已知存在楼层 f ,满足 0 <= f <= n ,任何从 高于 f 的楼层落下的鸡蛋都会碎,从 f 楼层或比它低的楼层落下的鸡蛋都不会破。
每次操作,你可以取一枚没有碎的鸡蛋并把它从任一楼层 x 扔下(满足 1 <= x <= n)。如果鸡蛋碎了,你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎,则可以在之后的操作中 重复使用 这枚鸡蛋。
请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少?
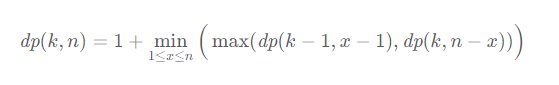
那为什么一定要max?
我想了快一天终于理解了
tip:鸡蛋如果没碎还可以捡起来继续丢
那假设在第i层丢鸡蛋,共有N层
为什么要把i-1的碎了的情况跟i+1到N两种情况取较大值?
为了求最坏情况下的最小取值
如现在有一百层楼,i为20
则i分为了0-19和21-100,如果直接取较小值就会导致计算出来的数据偏颇
更极端的情况下甚至出现i为1时,0-0和2-99,直接算出来最小取值为0的情况
而取较大值代表了该过程的所有最差情况累加到一起得到的最终计算次数
如果实际计算一定会低于这个次数,即使刚好命中最差情况也刚好是最小计算次数
并且通过min的范围遍历循环i
最终得到i落在哪点所算出的最差情况累加出来的最终次数最小
同理
leetcode上方案三的DP
也是假设一个点在x底部无限长,上方无限长,则蛋为i,投掷次数为k
此时投一次,假设有无数个蛋,有一部分会失败,有一部分会成功
失败的走到了f(i-1,k-1),成功的走到了f(i,k-1)
可以看出所有的失败和成功累加到一起再加1
就是在这个无限高的楼中所能覆盖到的楼高范围
即推出了DP

